Next: Direct Nonlinear Regression
Up: Estimating Parameters
Previous: Estimating Parameters
Divide equation (3) by 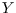 to get
to get
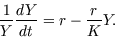 |
(5) |
Approximate
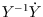 by the average rate of change between
observations divided by the average population between observations,
by the average rate of change between
observations divided by the average population between observations,
This gives a relationship between the right-hand-side of (5)
and your data. To be consistent 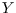 in the left-hand-side should also be
approximated using the average
in the left-hand-side should also be
approximated using the average
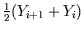 . Now, to get an
estimate for parameters
. Now, to get an
estimate for parameters 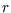 and
and 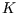 one should regress the data
one should regress the data
against the line
to determine 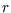 and
and 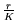 .
.
James Powell
2000-07-31
![]() to get
to get