


Next: Solution of the Logistic
Up: The Logistic Model
Previous: Conservation and Per-Capita Growth
It is more convenient to solve a single equation instead of both of
(1, 2), if possible. Fortunately, since both sides
of (1) are derivatives, it is dead easy to integrate this
equation. Let the initial conditions be given as 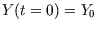 and
and
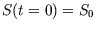 , and integrate both sides of (1):
, and integrate both sides of (1):
Notice that we have now solved for 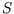 in terms of
in terms of 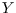 and known
quantities. Substituting this result into (2) gives
and known
quantities. Substituting this result into (2) gives
Now, if we define
we get the standard ecological form of the logistic equation:
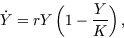 |
(3) |
where 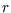 is the intrinsic growth rate of this population for this density
of sugar and
is the intrinsic growth rate of this population for this density
of sugar and 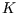 is the carrying capacity of this sugar solution.
is the carrying capacity of this sugar solution.
James Powell
2000-07-31
![]() and
and
![]() , and integrate both sides of (1):
, and integrate both sides of (1):
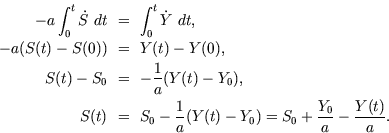
![\begin{eqnarray*}
\dot{Y} & \! = \! & b Y \left[ S_0+\frac{Y_0}{a}-
\frac{Y(t)...
...frac{b(a S_0+Y_0)}{a} Y \left[ 1 - \frac{Y}{(a S_0+Y_0)}\right].
\end{eqnarray*}](img19.gif)