
Up: Migration Problem - Biology
Previous: Parameters, Descriptions and Values
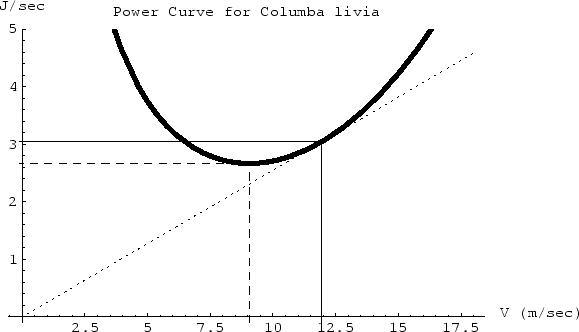
Figure 1:
Mechanical energy consumption curve (in bold) for a carrier pigeon of
mass 31 grams flying at about 400 m ASL. Location of absolute minimum power
consumption is illustrated by the dashed line; 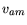 = 9.07 m/s. Location
of the maximum range speed, Vmr, located by use of a tangent line (small
dashes), is given by the solid lines. For this bird,
= 9.07 m/s. Location
of the maximum range speed, Vmr, located by use of a tangent line (small
dashes), is given by the solid lines. For this bird, 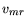 = 11.9 m/s.
Power required is 2.67 J/sec and 3.04 J/sec for
= 11.9 m/s.
Power required is 2.67 J/sec and 3.04 J/sec for 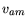 and
and 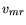 ,
respectively.
,
respectively.
 |
Let's work this out for a small common pigeon (Columba livia) which will
migrate at 400 meters of altitude. Here are measurements for the pigeon:
| Air Density (400 m) |
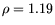 |
kilograms/cubic meter |
| Total Mass |
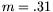 |
kilograms |
| Drag Coefficient |
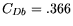 |
unit free |
| Body Area |
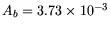 |
meters squared |
| Wing Disc Area |
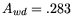 |
meters squared |
| Fat Fraction |
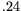 |
unit free |
We can calculate coefficients for the power curve:
and
The equation for mechanical power requirements is then
Energy required for a flight of distance 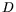 is
is
Taking a derivative to determine where the minimum 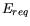 occurs,
occurs,
This can be solved for the maximum range speed, 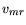 ,
,
The rate of energy consumption at this optimum speed is
See Figure 1 for a graphical depiction of this speed, the power curve,
and the overall minimum power speed.
On the other hand, the total energy available to the pigeon depends on its
stored fat. Since the fat fraction for this pigeon is 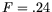 , the total mass
of the fat available is
, the total mass
of the fat available is 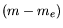 , which satisfy
, which satisfy
Thus
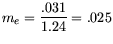 and therefore the mass of
fat is
and therefore the mass of
fat is
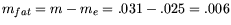 , or 6 grams of fat. Then the
energy
available is
, or 6 grams of fat. Then the
energy
available is
Therefore the time the pigeon can stay airborne at a speed of 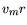 is
is
and the maximum distance the bird can travel is
or 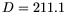 kilometers (about 132 miles).
kilometers (about 132 miles).


Up: Migration Problem - Biology
Previous: Parameters, Descriptions and Values
James Powell
2002-02-15


![]() , the total mass
of the fat available is
, the total mass
of the fat available is ![]() , which satisfy
, which satisfy