Next: The Exact Solution of
Up: Solution of the Gamblers
Previous: Definition and Exact Solution
The problem we need to solve in the previous section is a very close cousin to
a second order two point boundary value problem. These types of problems are
generally seen in an introductory course in ordinary differential equations.
In this section we will review just enough about two point boundary value
problems to allow us to determine a method for solving the finite difference
equation we have in the Gambler's Ruin problem.
Let's just start with an example of a linear, second order, constant coefficient
ordinary differential equation. The example will review the pertinent part of
the solution process.
Example 1
Consider the second order ordinary differential equation
with the initial conditions
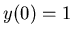
and
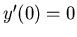
. Find the solution.
To find the solution we simply assume the solution form
Substituting into the differential equation gives the equation
Since the exponential function is never zero and the constant will be
assumed to be nonzero, the other factor must be zero. Thus we have
and thus the solution is
with the coefficients determined by the initial conditions.
The functions in Mathematica make it easy to solve the ordinary
differential equation in the above example. In particular, the command would
be
DSolve[ { y''[t]-3*y'[t]+y[t]==0, y[0]==1, y'[0]==0 }, y[t], t]
The syntax of the command is that the first argument must be a list of
equations. The second argument is the quantity you wish to solve for and the
third argument is the independent variable in the function. A more thorough
explanation of how to use this command is given in the appendices. This command
will do all the work including finding the unknown constants in the solution.
The homework problems at the end of the section include some solutions of
differential equations using DSolve.
Now let's consider a two point boundary value problem which is closely related
to the finite difference equation we are need to solve.
Example 2
Solve the differential equation
with
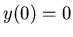
and
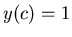
. If we apply the same process as above we will
obtain the quadratic equation
Solving gives
So the solution is given by
Applying the boundary conditions gives
We would finish the problem by computing the solution of the system of
equations for
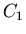
and
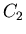
.
Again, we could us Mathematica to solve the ordinary differential equation
in the example above. The command would look like the following.
DSolve[ { p*y''[t]-y'[t]+(1-p)y[t]==0, y[0]==0, y[c]==1 }, y[t], t]
The output will be a form that is similar to the form above or can be
manipulated to that form. See the chapter notebook for the command the output of
the command.



Next: The Exact Solution of
Up: Solution of the Gamblers
Previous: Definition and Exact Solution
Joe Koebbe
2003-10-01