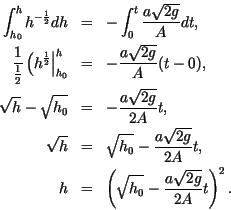Solution

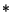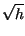To solve equation ($*$) we use separation of variables. First, divide both sides by $\sqrt{h}$ and multiply by 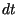$dt$ to separate 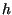$h$ from $t$:

$$\frac{dh}{\sqrt{h}} = -\frac{a\sqrt{2 g}}{A} dt,$$

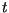and now integrate both sides with respect to their variables. We will need to use initial conditions as the bottom limits of integration, so let the initial height at time zero be 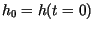$h_0 = h(t=0)$. Then:

$$\begin{eqnarray*} \int_{h_0}^h h^{-\frac12} dh & = & - \int_0^t \frac{a\sqrt{2 g... ... h & = & \left(\sqrt{h_0} - \frac{a\sqrt{2 g}}{2A} t \right)^2. \end{eqnarray*}$$

As a natural consequence of this solution one can calculate the predicted time for the bucket to empty by setting 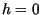$h=0$ above, which gives

$$\sqrt{h_0} - \frac{a\sqrt{2 g}}{2A} t = 0,$$

or

$$t_{\mbox{\tiny empty}} = \frac{2A\sqrt{h_0}}{a\sqrt{2 g}} = \frac{A\sqrt{2 h_0}}{a\sqrt{g}}.$$