Next: Solution
Up: The Torricelli Model
Previous: The Torricelli Model
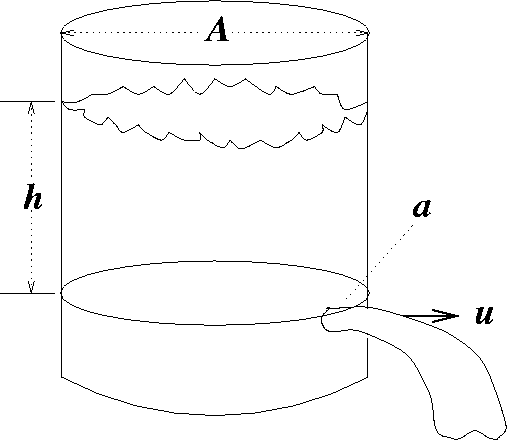
The Torricelli model for the draining bucket is based on two physical
concepts:
- The Bernoulli relationship between pressure,
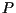 , density,
, density, 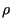 and speed,
and speed, 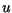 for fluid along a streamline:
for fluid along a streamline:
- The hydrostatic relationship between changes in pressure over the
height of a fluid column and gravity (acceleration
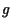 ), fluid density
), fluid density
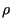 and the height
and the height 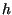 of the column:
of the column:
Equating these two gives a relationship between height of the
fluid above
the hole and the speed at which it spews forth,
The because the volume lost of fluid in the bucket must equal the flux of
fluid through the bucket's hole (with area 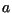 ),
),
and using the fact that (for a bucket with regular sides and constant cross
section in height) 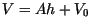 ,
,
Substituting in the relationship 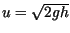 from above gives a
differential equation for height of the fluid,
from above gives a
differential equation for height of the fluid, 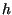 , as a function of time:
, as a function of time:



Next: Solution
Up: The Torricelli Model
Previous: The Torricelli Model
James Powell
2000-07-30