


Next: Disease Dynamics
Up: Games to Teach Mathematical
Previous: References
In this appendix we present the rules for the Predator Prey game. Students
develop a game which captures the major effects of predation between two
species, altering the rules of the game to reflect increasingly complex
interactions, and involve themselves in building models of their toy
ecologies. Our objectives for this exercise are to
- Produce model ecologies which reproduce bunny-coyote population
oscillations in the intermountain region.
- Learn how to build various discrete and continuous models of `real'
data sets.
- Explore the practical meaning of various changes to ecosystems and
characteristics of species.
We divide into groups of three. Each member of the group will be
responsible for Predators, Prey, and Administration by turns. The goals
for the meta-game experience are to alter the rules of the game to produce
the most `realistic' model ecology with a minimum set of rules, beginning
with the simple rules described below. Here are the specific
responsibilities to be considered in the meta-game:
- Decide on and record the current rules for the game.
- Iterate the game for at least ten turns, collecting data on the
populations of predator and prey at each turn.
- Evaluate the `reality' of this data set with the current set of
rules. Record what the problems are.
- Discuss what to change about the rules of the game. Options may
include:
- Rates of predation, reproduction, death....
- Handling time, saturability, functional responses....
- Structure of the environment: refuges, nearest neighbors,
numbers per hex....
- Step size, seasonality, Elvis sightings....
Record what you have changed and why. - Change who does what and return to first step.
Here are the beginning rules for the predator-prey game, with no guarantee
that they work at all, but they do give us a starting point. Let 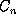 and
and 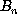 denote the number of coyotes and bunnies at game turn n.
Below are the rules for your first iteration of the Predator-Prey game.
First, pick initial values for
denote the number of coyotes and bunnies at game turn n.
Below are the rules for your first iteration of the Predator-Prey game.
First, pick initial values for 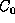 and
and 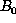 . Then:
. Then:
- Predator and Prey players allocate their species,
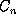 and
and 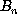 , one per hex, on
their game board, placing a red X for predator, a blue 0 for prey.
, one per hex, on
their game board, placing a red X for predator, a blue 0 for prey. - Overlay the transparencies (prey on top). Count the number of
hexes which include both a predator and prey.
- Calculate predator-prey interactions. For the bunnies:
- The number of eaten bunnies is equal to the number of
overlaps. Subtract eaten bunnies from population.
- Surviving bunnies can reproduce. Double the population of
surviving bunnies.
- This is now
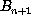 .
. - Record
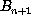 .
.
For the coyotes:
- All of the eaten bunny-units become fuzzy baby coyotes.
- Lose one-quarter of the original population (round the
losses down), then add in the F.B.Cs.
- This is now
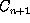 .
. - Record
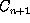 .
.
- Return to the re-allocation phase with the (n+1)st values available
for distribution.
If either of the populations becomes zero or less the species has gone
extinct.
The following is the outline for a group-homework on discrete models.
- Refine the rules of your predator-prey game to produce oscillations,
including the following:
- Nontrivial topology (perhaps altering the structure of the
hex map so that only certain numbers of a species can live
there, or to create internal `edges' to lower the number of
`nearest neighbors'.
- A `refuge' for the prey.
- A density-dependent response (for example, each bunny needs a
certain number of hexes to live).
- Build a discrete model for your ecology, and analyze the fixed points
and their stability.
- Try out the game with your rules, in particular using some initial
conditions near any fixed points in your model above.
- How do the two compare? If they differ, can you tell why they
differ? Are the oscillations due to the structure of your model,
or to stochastic variations?
- Prepare an informal group presentation to the rest of the class on
your efforts. It need not be tremendously formal, but your group
should be prepared to exhibit some overhead illustrations of both
the game and model outputs.



Next: Disease Dynamics
Up: Games to Teach Mathematical
Previous: References
James Powell
Tue Feb 18 12:21:04 MST 1997
![]() and
and ![]() denote the number of coyotes and bunnies at game turn n.
Below are the rules for your first iteration of the Predator-Prey game.
First, pick initial values for
denote the number of coyotes and bunnies at game turn n.
Below are the rules for your first iteration of the Predator-Prey game.
First, pick initial values for ![]() and
and ![]() . Then:
. Then: