


Next: Project Goals
Up: Modelling Diseases - Continuous
Previous: Modelling Diseases - Continuous
Let 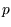 be the fraction of a mixing populace which is infected with a
disease. Then
be the fraction of a mixing populace which is infected with a
disease. Then 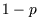 is the fraction of the population which is
susceptible, and a model for
is the fraction of the population which is
susceptible, and a model for 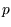 changes in time is
changes in time is
where 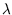 captures the rate of transmission of the disease in the
population and
captures the rate of transmission of the disease in the
population and 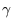 reflects the recovery of the infectious population.
For different diseases and different mixing populations,
reflects the recovery of the infectious population.
For different diseases and different mixing populations, 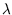 and
and
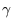 will vary.
will vary.
James Powell
2000-07-28
![]() be the fraction of a mixing populace which is infected with a
disease. Then
be the fraction of a mixing populace which is infected with a
disease. Then ![]() is the fraction of the population which is
susceptible, and a model for
is the fraction of the population which is
susceptible, and a model for ![]() changes in time is
changes in time is